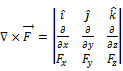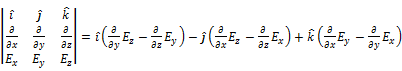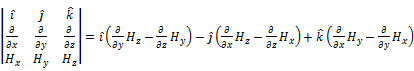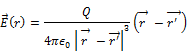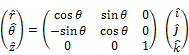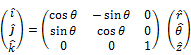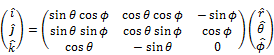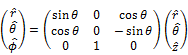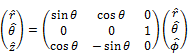Contents
Tangent, Normal & Bi-normal of Space Curves
Differentials in cylindrical & Spherical System
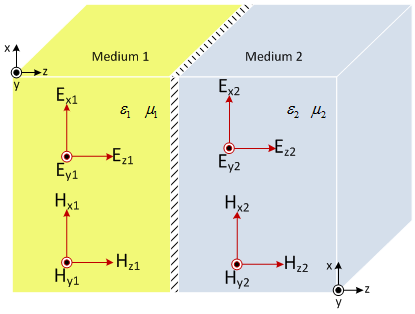
Introduction to Boundary Conditions
Parallel polarization (TM Polarization)
Perpendicular polarization (TE Polarization)
|
Dot Product |
|
|
Commutative |
|
Cross Product |
|
|
Non-commutative |
|
Gradient |
|
|
· Gradients works on scalar functions. · Gradient of a function gives a vector · It is rate of change of a function (with information about directions) |
|
Divergence |
|
|
· Divergence works on vector functions. · Divergence of a functions gives a scalar · It is rate of change of a function (without information about directions) |
|
Curl |
|
|
· Curl works on vector functions. · Curl of a functions gives a vector. · It is measure of rotational ability of a function (with information about directions) |
|
Directional
Derivative of function F along |
|
|
|
|
Directional
Derivative of function F along |
|
|
|
|
Triple Product |
The best way to remember this rule is by using outer-middle-inner terms
|
|
|
|
|
|
|
|
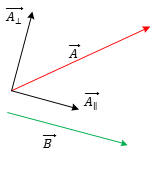
Consider two vectors |
|
|
|
Parallel Projection : Vector
Component of
|
|
|
|
Normal Projection : Vector
Component of |
|
Since
|
|
Given a vector |
|
|
Parallel to |
|
|
Perpendicular to |
|
|
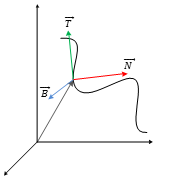
Given a space curve defined by
the vector the Tangent vectors to any point on the space curve is |
|
|
Normal vector to any point on the curve |
|
|
Electric field due to a point
charge
|
|
|
Electric field due to line
charge distribution
|
|
|
Electric field due to surface
charge distribution |
|
Mangnetostatics Basics
Coordiante systems
|
Cylindrical Coordinate Systems |
|
|
|
Spherical Coordinate System |
|
|
|
Cylindrical
|
|
|
Cartesian |
|
|
Spherical |
|
|
Cartesian |
|
|
Spherical |
|
|
Cylindrical |
|
http://en.wikipedia.org/wiki/Del_in_cylindrical_and_spherical_coordinates
|
Coordinate System |
Elemental Surface area |
|
Cylindrical System
Surface area of the elemental
volume |
Note: |
|
Spherical System
Surface area of the elemental
volume |
|
|
Coordinate System |
Elemental Volume |
|
Cylindrical |
|
|
Spherical |
|
|
Coordinate System |
Elemental Arc Length |
Scale Factors |
|
Cylindrical |
|
|
|
Spherical |
|
|
Given a
space curve ![]() as shown in the
figure the correspondingtangent vector
as shown in the
figure the correspondingtangent vector ![]() , normal vector
, normal vector ![]() and
and
bi-normal
unit vector ![]()
|
|
|
Parametric Equation
of a line from ![]() to
to ![]()
![]() ;
; ![]()
|
|
Vector Form |
Parametric Form |
|
Equation of a line
parallel to vector and passing through the point |
|
|
|
Equation of a line passing
through the points |
Here the range of |
Here the range of |
|
Equation of a plane
perpendicular to vector and passing through the point |
|
|
|
|
|
|
|
Orthogonal |
Cylindrical |
|
|
|
|
|
|
|
|
|
|
MAXWELLS EQUATION |
Derivative Form |
Integral Form |
Using phasors and complex permittivity |
|
Gauss's Theorem |
|
|
|
|
Gauss's Theorem (in magnetism) |
|
|
|
|
Ampere's Law |
|
|
|
|
Faraday's Law |
|
|
|
|
In
static case |
Electrostatics/ Magneto statics |
|
Gauss's Theorem |
|
|
Gauss's Theorem (in magnetism) |
|
|
Ampere's Law |
|
|
Faraday's Law |
|
|
Magnetic Field Intensity |
|
|
Electric field intensity |
|
|
Electric potential |
|
|
Magnetic potential |
|
|
Continuity Equation |
|
|
Laplace's Equation |
|
|
Poisson's Equation |
|
|
Ohm's Point Law |
|
|
Conduction Current density |
|
|
Displacement Current density |
|
|
Intrinsic Impedance |
|
|
Velocity in any media |
|
|
Relation
between |
|
The three
constitutive parameter of a medium are ![]()
Complex
permittivity is defined as ![]()
|
|
|
|
Properties of the medium |
Wave Equation |
Propagation Constant |
|
Charge free medium |
|
|
|
Charge free and Loss-less medium
|
|
|
|
General wave equations
:
For a uniform plane in x-y
|
|
|
Set of wave equations Click here for derivation obtained from general wave equations
|
|
|
The general solution of the wave equation is of the form
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
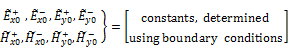
Assuming that ![]() has component only along x-direction and is travelling along +
z-direction, we have
has component only along x-direction and is travelling along +
z-direction, we have
![]()
![]()
![]()
![]()
![]()
![]()
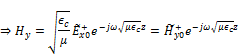
![]()
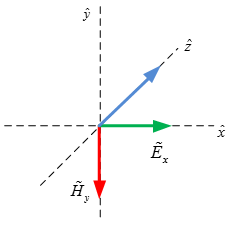
Use right hand rule for direction
|
|
|
|
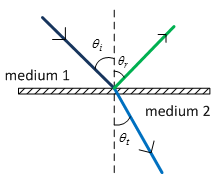
SNELL'S LAW
Refractive index of a medium ( |
|
|
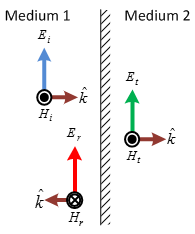
Electromagnetic Reflection and Transmission for Normal Incidence
·
Transmission
coefficient
·
Reflection
coefficient
·
·
Ratio of
powers . Replace |
|
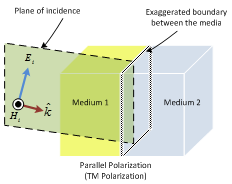
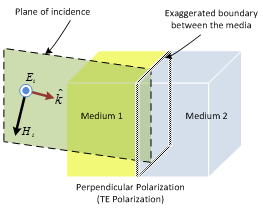
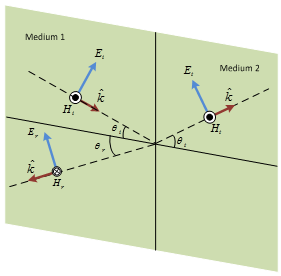
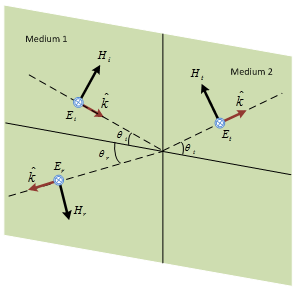
It is a plane containing 1) direction of propagation and 2) normal to the boundary between the two surfaces.
Electric field is parallel to the plane of incidence.
Electric filed is normal to the plane of incidence
|
PARALLEL POLARIZATION |
PERPENDICULAR POLARIZATION |
|
|
|
|
|
|
|
|
|
|
LINEAR |
|
|
|
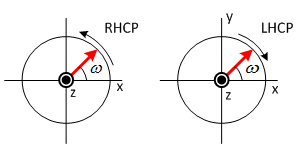
CIRCULAR |
Since
|
|
|
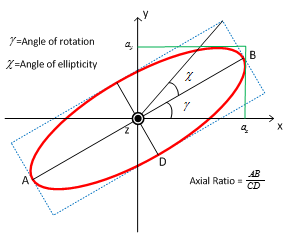
ELLIPTICAL |
If χ is +ve=LHCP If χ is −ve=RHCP
|
·
·
2 values of
·
If ·
If ·
|
Inductors
|
Faradays Law |
|
|
Flux |
|